최대공약수와 최소공배수는 어떻게 구할까?
유클리드 호제법 (Euclidean Algorithm)
--
유클리드 호제법은
두 수의 최대공약수(GCD)를 효율적으로 구하는 알고리즘이지만,
해당 최대공약수(GCD)를 이용해서 최소공배수(LCM)도 쉽게 구할 수 있기 때문에
둘 다 구하는 알고리즘이라고도 할 수 있다.
정확히는
두 정수의 최대공약수(GCD)를 구하는 효율적인 알고리즘으로
두 수의 최대공약수를 구할 때, 나눗셈을 반복적으로 수행하여 나머지가 0이 될 때까지 계산하는 방법이다.
--
최대공약수 (GCD)
--
공식
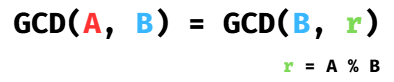
위 공식을 이용하여
r = 0이 될 때 B가 최대공약수(GCD)가 된다.
증명
A / B = q + r
=> A = B * q + r
- A > B 가정
- q = 몫
- r = 나머지
GCD(A, B) = GCD(B, r)
위 조건이 성립하기 위한 증명 2가지
- d(공약수)로 A와 B를 나누면, r도 나눌 수 있다.
- d(공약수)로 B와 r을 나누면 A도 나눌 수 있다.
d가 A와 B의 "공약수"라면?
A = d * x
B = d * y
A / B = q + r
=> r = A - B * q
=> r = (d * x) - (d * y) * q
=> r = d(x - yq)
즉, r 또한 d(공약수)로 나눌 수 있다.
그래서 d는 GCD(B, r)의 공약수도 될 수 있는 것이다.
r = 0이 되는 순간의 B가 최대공약수인 이유
유클리드 호제법 동작 과정
- A를 B로 나눈 나머지를 구함 (A % B)
- A를 B로 변경, B를 (A % B) 나머지로 변경
- 이를 반복하여 나머지가 0이 될 때까지 진행
- 나머지가 0이 되는 순간의 B는 최대공약수
GCD(48, 18)
= GCD(18, (48 % 18)) = GCD(18, 12)
= GCD(12, (18 % 12)) = GCD(12, 6)
= GCD(6, (12 % 6)) = GCD(6, 0)
B = 6 = 최대공약수
나머지가 0이라는 것은
6으로 나누면 기존 B(18)이 0으로 깔끔하게 나누어진다는 것이며
정확히는 A가 B로 나누어 떨어진다는 의미고
이때의 B가 더 이상 나눌 수 없는 가장 큰 공약수가 된다.
--
최소공배수 (LCM)
--
공식
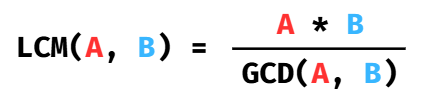
--
'Record > 알고리즘 풀이' 카테고리의 다른 글
| [ Lv.0 / 산술 ] 배열의 평균값 (+ Stream API) (0) | 2024.08.24 |
|---|---|
| [ Lv.0 / 산술 ] 나이 출력 (+ 변수 생략 후 바로 계산 및 출력 ) (0) | 2024.08.23 |
| [ Lv.0 / 비교 ] 숫자 비교하기 (+ if문, 삼항 연산자 ) (0) | 2024.08.23 |
