그래프는 무엇일까?
그래프 (graph)
--
그래프는
노드의 집합과 간선(edge, 엣지)의 집합으로 구성된다.
노드(node)는
그래프의 기본 요소로, 보통 정점(Vertex)이라고도 부른다.
각 노드는 데이터를 저장할 수 있으며, 다른 노드와의 관계를 나타내는 엣지에 의해 연결된다.
엣지(Edge)는
두 노드를 연결하는 선으로, 노드 간의 관계나 연결을 표현한다.
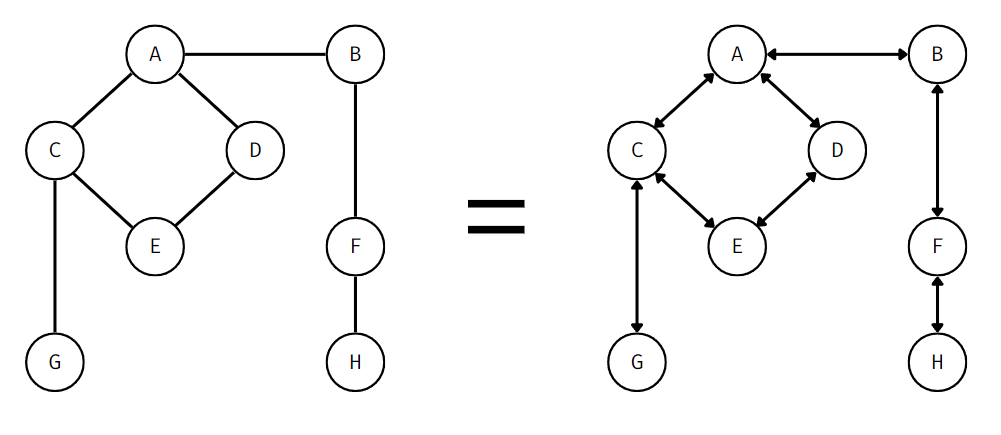
엣지는 방향이 있는 경우와 없는 경우가 존재한다.
- 방향이 없는 엣지는 무방향 엣지(Undirected Edge)라고 부르며 보통 양방향을 의미한다.
(무방향 엣지로 이루어진 그래프를 무향 그래프 (Undirected Graph)라고 부른다.)
- 방향이 있는 엣지는 유방향 엣지(Directed Edge)라고 부르며 해당 방향을 가리키는 의미다. (일방통행)
(유방향 엣지로 이루어진 그래프를 유향 그래프 (Directed Graph)라고 부른다.)
CS에서 기본적인 자료 구조에 속하며,
다양한 문제와 프로그래밍 작업에서 그래프가 생기게 된다.
즉, 다른 자료 구조들과 다르게 그래프 구조는
특정 계산을 최적화하기 위해 설계된 것이 아니라 데이터 자체로부터 자연스럽게 발생한 것이다.
(그래프는 자신이 나타내는 데이터를 반영한 것)
그래프 구조는
사회관계망 (노드 = 사람, 간선(엣지) = 사람들 사이의 관계),
교통망 (노드 = 도시, 간선(엣지) = 경로),
네트워크 (노드 = 컴퓨터, 간선(엣지) = 컴퓨터 사이의 연결)
등을 포함하는 많은 실제 시스템과 비슷하므로
그래프 알고리즘은 시각화할 때 유용하다.
그래프의 간선(엣지)에서
무방향(양방향)은 대부분 두 노드 간의 원활한 양방향 관계를 나타내고
유방향(단방향)은 일방통행 도로처럼 한 방향으로의 흐름을 나타낸다.
이때 유방향 간선은 두 노드 상이의 의존 관계(dependency)와 같은 추상적인 문제를 모델링할 수 있게 해 준다.
예시) 토마토 스파게티를 만들기 위한 과정을 그래프로 만들기

각 노드는 과정의 단계들이 포함되어 있으며
간선(엣지)는 해당 단계들 상이의 의존 관계를 나타낸다.
(물 버리기를 하기 위해서는 면을 먼저 삶아야 한다는 의미)
(면 삶기와 소스 데우기 사이에는 간선이 필요하지 않다.)
그래프에서 간선(엣지)에 가중치(weight)를 부여하게 되면 그래프의 모델링 능력이 더 커진다.
가중치가 있는 간선은 노드의 연결 유무뿐 아니라 해당 연결의 비용까지도 나타낸다.
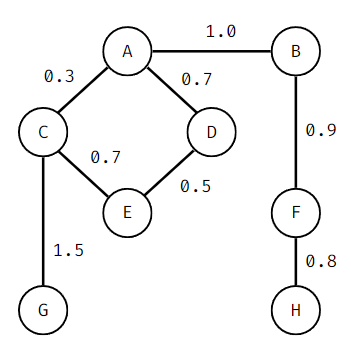
그래프 표현하기
그래프의 추상적인 구조는 상대적으로 간단하지만,
컴퓨터 메모리에 노드와 간선을 표현하는 방법은 다양하다.
가장 흔한 두 가지 방법
- 인접 행렬(adjacency matrix)
- 인접 리스트(adjacency list)
위 두가지 표현 방법은 방향성이 있거나 없는 간선이나,
가중치가 있거나 없는 간선을 모두 다룰 수 있다.
인접 리스트 형식은
이웃을 노드마다 별도의 리스트로 저장한다.
(노드 복합 자료 구조 내에서 이웃들을 표현하는 배열이나 연결 리스트를 사용할 수 있다.)
각 노드 클래스(구성) [JAVA]
public class Node {
private String name;
private List<Node> neighbors; // 현재 노드와 인접한 노드들
public Node(String name) {
this.name = name;
this.neighbors = new ArrayList<>();
}
}
간선에 대한 추가 정보를 저장하는 각 노드 클래스(구성) [JAVA]
class Edge {
private int toNode;
private int fromNode;
private float weight; // 가중치
public Edge(int toNode, int fromNode, float weight) {
this.toNode = toNode;
this.fromNode = fromNode;
this.weight = weight;
}
}
class Node {
private String name;
private int id; // 해당 노드의 고유 id
private List<Edge> edges; // 해당 노드에 연결된 간선들
public Node(String name, int id) {
this.name = name;
this.id = id;
this.edges = new ArrayList<>();
}
}
그래프 클래스(구조) [JAVA]
(간선 자료 구조를 만들든 말든, 그래프는 노드들로 이뤄진 배열(리스트)을 포함해야 한다.)
class Graph {
private int numNodes;
private List<Node> nodes;
public Graph(int numNodes) {
this.numNodes = numNodes;
this.nodes = new ArrayList<>();
}
}
구현 방법과는 관계없이
노드에 연결된 이웃 노드 목록을 통해 주어진 노드의 이웃에 접근할 수 있다.
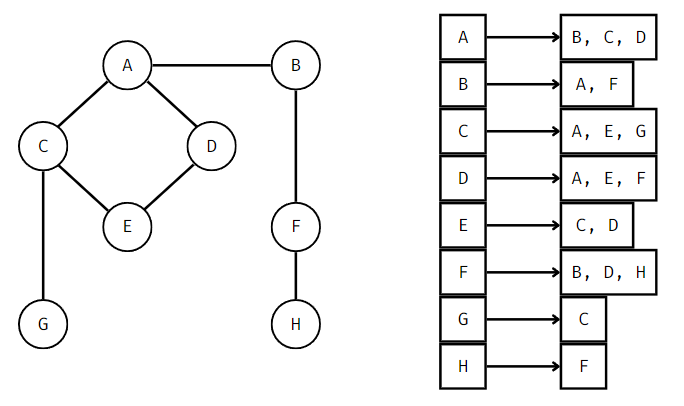
방향성(단방향) 간선의 경우
노드의 간선 목록이나 이웃 노드 목록은 해당 노드에서 떠나가는 간선만 포함해야 한다.
ex) A에는 B로 향하는 간선이 있어도 B에는 A로 향하는 간선이 없을 수 있다.
(위 그림은 양방향 간선이기 때문에 A에서도 B로 향하는 간선이 있고, B에서 A로 향하는 간선이 있다.)
이렇게 인접 리스트는
사회관계망 같은 실제 상황을 반영하여 이웃에 대한 지역적인 시각을 제공한다.
각 노드는 자신과 연결된 노드만 추적하는데
이는 사회관게망에서 개인은 친구로 인정하는 사람들을 결정하여 자신만의 연결 목록을 유지하는 것과 비슷하다.
반면, 인접 행렬은 그래프를 행렬로 나타낸다.
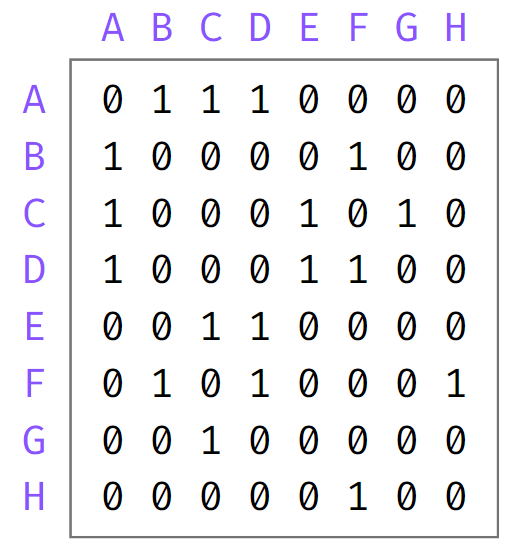
위 그림처럼 노드마다 행과 열이 하나씩 할당되고
특정 행★, 열☆의 값은 노드 ★에서 노드 ☆로 가는 간선의 가중치를 나타낸다.
(행A, 열C 가 가리키는 값은 노드 A에서 노드 C로 가는 간선의 가중치다.)
가중치가 0이면
해당 방향의 간선이 존재하지 않다는 의미다.
--
그래프는 무엇일까?
그래프 (graph)
--
그래프는
노드의 집합과 간선(edge, 엣지)의 집합으로 구성된다.
노드(node)는
그래프의 기본 요소로, 보통 정점(Vertex)이라고도 부른다.
각 노드는 데이터를 저장할 수 있으며, 다른 노드와의 관계를 나타내는 엣지에 의해 연결된다.
엣지(Edge)는
두 노드를 연결하는 선으로, 노드 간의 관계나 연결을 표현한다.
엣지는 방향이 있는 경우와 없는 경우가 존재한다.
- 방향이 없는 엣지는 무방향 엣지(Undirected Edge)라고 부르며 보통 양방향을 의미한다.
(무방향 엣지로 이루어진 그래프를 무향 그래프 (Undirected Graph)라고 부른다.)
- 방향이 있는 엣지는 유방향 엣지(Directed Edge)라고 부르며 해당 방향을 가리키는 의미다. (일방통행)
(유방향 엣지로 이루어진 그래프를 유향 그래프 (Directed Graph)라고 부른다.)
CS에서 기본적인 자료 구조에 속하며,
다양한 문제와 프로그래밍 작업에서 그래프가 생기게 된다.
즉, 다른 자료 구조들과 다르게 그래프 구조는
특정 계산을 최적화하기 위해 설계된 것이 아니라 데이터 자체로부터 자연스럽게 발생한 것이다.
(그래프는 자신이 나타내는 데이터를 반영한 것)

그래프 구조는
사회관계망 (노드 = 사람, 간선(엣지) = 사람들 사이의 관계),
교통망 (노드 = 도시, 간선(엣지) = 경로),
네트워크 (노드 = 컴퓨터, 간선(엣지) = 컴퓨터 사이의 연결)
등을 포함하는 많은 실제 시스템과 비슷하므로
그래프 알고리즘은 시각화할 때 유용하다.
그래프의 간선(엣지)에서
무방향(양방향)은 대부분 두 노드 간의 원활한 양방향 관계를 나타내고
유방향(단방향)은 일방통행 도로처럼 한 방향으로의 흐름을 나타낸다.
이때 유방향 간선은 두 노드 상이의 의존 관계(dependency)와 같은 추상적인 문제를 모델링할 수 있게 해 준다.
예시) 토마토 스파게티를 만들기 위한 과정을 그래프로 만들기

각 노드는 과정의 단계들이 포함되어 있으며
간선(엣지)는 해당 단계들 상이의 의존 관계를 나타낸다.
(물 버리기를 하기 위해서는 면을 먼저 삶아야 한다는 의미)
(면 삶기와 소스 데우기 사이에는 간선이 필요하지 않다.)
그래프에서 간선(엣지)에 가중치(weight)를 부여하게 되면 그래프의 모델링 능력이 더 커진다.
가중치가 있는 간선은 노드의 연결 유무뿐 아니라 해당 연결의 비용까지도 나타낸다.

그래프 표현하기
그래프의 추상적인 구조는 상대적으로 간단하지만,
컴퓨터 메모리에 노드와 간선을 표현하는 방법은 다양하다.
가장 흔한 두 가지 방법
- 인접 행렬(adjacency matrix)
- 인접 리스트(adjacency list)
위 두가지 표현 방법은 방향성이 있거나 없는 간선이나,
가중치가 있거나 없는 간선을 모두 다룰 수 있다.
인접 리스트 형식은
이웃을 노드마다 별도의 리스트로 저장한다.
(노드 복합 자료 구조 내에서 이웃들을 표현하는 배열이나 연결 리스트를 사용할 수 있다.)
각 노드 클래스(구성) [JAVA]
public class Node {
private String name;
private List<Node> neighbors; // 현재 노드와 인접한 노드들
public Node(String name) {
this.name = name;
this.neighbors = new ArrayList<>();
}
}
간선에 대한 추가 정보를 저장하는 각 노드 클래스(구성) [JAVA]
class Edge {
private int toNode;
private int fromNode;
private float weight; // 가중치
public Edge(int toNode, int fromNode, float weight) {
this.toNode = toNode;
this.fromNode = fromNode;
this.weight = weight;
}
}
class Node {
private String name;
private int id; // 해당 노드의 고유 id
private List<Edge> edges; // 해당 노드에 연결된 간선들
public Node(String name, int id) {
this.name = name;
this.id = id;
this.edges = new ArrayList<>();
}
}
그래프 클래스(구조) [JAVA]
(간선 자료 구조를 만들든 말든, 그래프는 노드들로 이뤄진 배열(리스트)을 포함해야 한다.)
class Graph {
private int numNodes;
private List<Node> nodes;
public Graph(int numNodes) {
this.numNodes = numNodes;
this.nodes = new ArrayList<>();
}
}
구현 방법과는 관계없이
노드에 연결된 이웃 노드 목록을 통해 주어진 노드의 이웃에 접근할 수 있다.

방향성(단방향) 간선의 경우
노드의 간선 목록이나 이웃 노드 목록은 해당 노드에서 떠나가는 간선만 포함해야 한다.
ex) A에는 B로 향하는 간선이 있어도 B에는 A로 향하는 간선이 없을 수 있다.
(위 그림은 양방향 간선이기 때문에 A에서도 B로 향하는 간선이 있고, B에서 A로 향하는 간선이 있다.)
이렇게 인접 리스트는
사회관계망 같은 실제 상황을 반영하여 이웃에 대한 지역적인 시각을 제공한다.
각 노드는 자신과 연결된 노드만 추적하는데
이는 사회관게망에서 개인은 친구로 인정하는 사람들을 결정하여 자신만의 연결 목록을 유지하는 것과 비슷하다.
반면, 인접 행렬은 그래프를 행렬로 나타낸다.

위 그림처럼 노드마다 행과 열이 하나씩 할당되고
특정 행★, 열☆의 값은 노드 ★에서 노드 ☆로 가는 간선의 가중치를 나타낸다.
(행A, 열C 가 가리키는 값은 노드 A에서 노드 C로 가는 간선의 가중치다.)
가중치가 0이면
해당 방향의 간선이 존재하지 않다는 의미다.
--
