이진 탐색이란?
선형 스캔
--
선형 스캔은
이진 탐색보다 더 간단한 알고리즘으로
리스트에서 한 번에 하나씩 값을 목푯값과 비교하면서 목푯값을 찾거나 목록의 끝에 도달할 때까지 비교하여 목푯값을 찾는 것이다.
즉, 리스트 내부의 처음부터 끝까지 직접 목푯값과 비교하여 찾는 방식이다.
리스트(배열)에서 '3'을 찾는 선형 스캔 알고리즘 예시 코드 [JAVA]
public class LinearScan {
public static int linearScan(int[] A, int target) {
int i = 0;
while (i < A.length) {
if (A[i] == target) {
return i; // 리스트에서 목푯값을 찾으면 해당 위치 인덱스 반환
}
i = i + 1;
}
return -1; // 만약 리스트에 목푯값이 존재하지 않으면 -1 반환
}
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5};
int target = 3;
int result = linearScan(array, target);
. . .
}
}
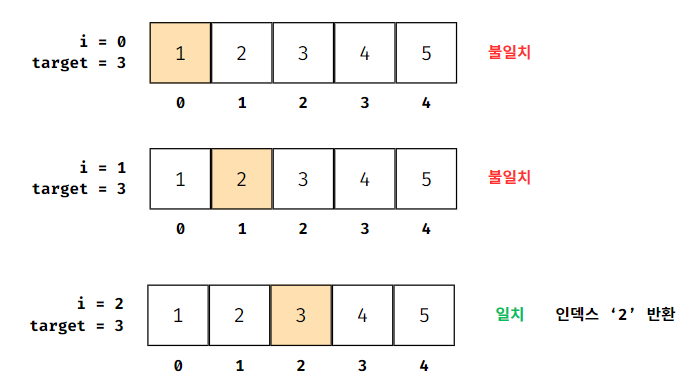
이렇게 선형 스캔 알고리즘은
리스트의 모든 항목을 직접 비교를 해야하기 때문에 "무식하게 검사하는 방법"으로
위 예시처럼 리스트의 크기가 작으면 괜찮지만
리스트의 크기가 커질수록 비효율적이다.
--
이진 탐색
--
이진 탐색은
(오름차순으로) 정렬된 리스트에서 목푯값을 찾는 알고리즘으로
리스트를 절반으로 분할하고 목푯값이 어느 쪽 절반에 속하는지 결정하는 것을 마지막 값만 남을 때까지 반복한다.
이때 현재 활성화된 탐색 공간(배열)에서 '상계'와 하계'라는 단어도 사용한다.
- 상계 (upper bound) : 현재 활성화된 탐색 공간에 속하는 배열에서 가장 높은 인덱스를 의미
- 하계 (lower bound) : 현재 활성화된 탐색 공간에 속하는 배열에서 가장 낮은 인덱스을 의미
이진 탐색을 매 번 반복할 때마다 현재 활성화된 탐색 공간(배열)의 중간 지점 값을 선택하며 진행한다.
IndexMid = (IndexHigh + IndexLow) / 2
이렇게 중간 지점을 구하고 IndexMid에 위치하는 값과 찾고자하는 목푯값과 비교하여
목푯값이 IndexMid에 위치하는 값보다 작다면 IndexMid를 기준으로 왼쪽 탐색 공간(배열)을 탐색하고
크다면 오른쪽 탐색 공간(배열)을 탐색한다.
만약 같다면 즉시 탐색을 완료한다.
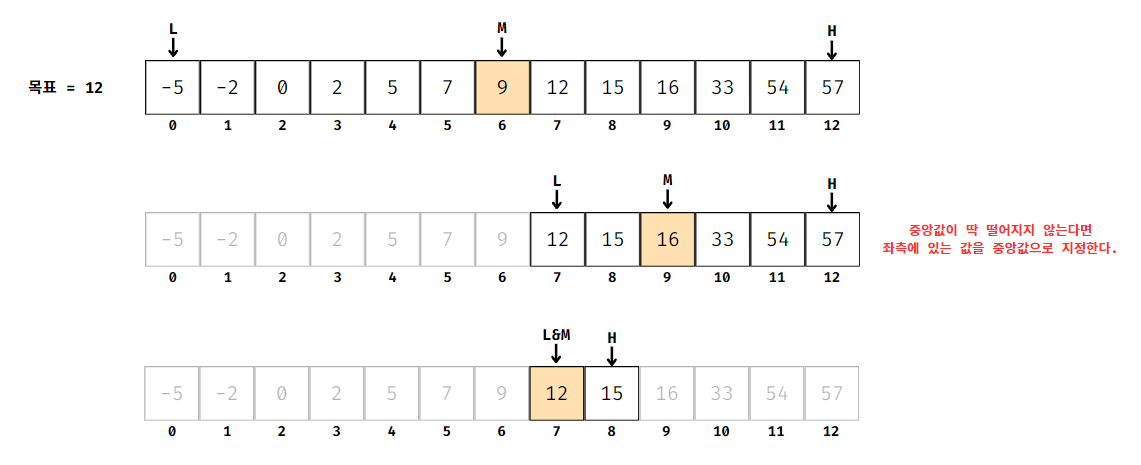
- 현재 활성화된 탐색 공간에서 하계(L)와 상계(H)를 기준으로
중간 지점을 지정(인덱스 = 6)하고 해당 중앙값을 목푯값인 12와 비교.
중앙값보다 목푯값이 크기 때문에 중앙값을 포함하여 좌측 리스트 공간에는 목푯값이 존재하지 않는다고 판단.
우측 리스트만 활성화를 하기 위해 하계를 인덱스 7로 이동. - 변경된 L과 H를 기준으로 중간 지점을 다시 지정(인덱스 = 8)하고 중앙 값을 목푯값인 12와 비교.
중앙값보다 목푯값이 작기 때문에 중앙값을 포함하여 우측 리스트 공간에는 목푯값이 존재하지 않는다고 판다.
좌측 리스트만 활성화를 하기 위해 상계를 인덱스 7로 이동. - 변경된 L과 H를 기준으로 중간 지점을 다시 지정(인덱스 = 7)하고 중앙 값을 목푯값인 12와 비교.
해당 중앙 값이 목푯값과 일치하므로 탐색 완료.
중간 지점을 지정할 때 딱 떨어지지 않는다면 중간 지점에서 좌측에 있는 공간을 중앙값으로 지정한다.
이진 탐색 알고리즘 예시 코드 [JAVA]
public class BinarySearch {
public static int binarySearch(int[] A, int target) {
// 초기 상계와 하계 지정
int indexHigh = A.length - 1;
int indexLow = 0;
while (indexLow <= indexHigh) {
// 중간 지점 계산 (소숫점이 나온다면 해당 소숫점 생략 = 좌측 중간 지점 선택)
int indexMid = (indexHigh + indexLow) / 2;
if (A[indexMid] == target) {
return indexMid;
} else if (A[indexMid] < target) {
indexLow = indexMid + 1;
} else {
indexHigh = indexMid - 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] array = {-5, -2, 0, 2, 5, 9, 12, 15, 16,33, 54, 57};
int target = 12;
int result = binarySearch(array, target);
}
}--
'CS > 자료구조' 카테고리의 다른 글
| 이진 탐색 트리 (0) | 2024.08.05 |
|---|---|
| 스택과 큐 (+ 깊이 우선 탐색, 너비 우선 탐색) (0) | 2024.08.03 |
| 동적 자료 구조 (+ 연결 리스트) (0) | 2024.08.02 |
| 데이터를 메모리에 저장하기 ( + 배열의 삽입 정렬 ) (0) | 2024.07.31 |
| 자료구조란? (0) | 2024.07.30 |
이진 탐색이란?
선형 스캔
--
선형 스캔은
이진 탐색보다 더 간단한 알고리즘으로
리스트에서 한 번에 하나씩 값을 목푯값과 비교하면서 목푯값을 찾거나 목록의 끝에 도달할 때까지 비교하여 목푯값을 찾는 것이다.
즉, 리스트 내부의 처음부터 끝까지 직접 목푯값과 비교하여 찾는 방식이다.
리스트(배열)에서 '3'을 찾는 선형 스캔 알고리즘 예시 코드 [JAVA]
public class LinearScan {
public static int linearScan(int[] A, int target) {
int i = 0;
while (i < A.length) {
if (A[i] == target) {
return i; // 리스트에서 목푯값을 찾으면 해당 위치 인덱스 반환
}
i = i + 1;
}
return -1; // 만약 리스트에 목푯값이 존재하지 않으면 -1 반환
}
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5};
int target = 3;
int result = linearScan(array, target);
. . .
}
}

이렇게 선형 스캔 알고리즘은
리스트의 모든 항목을 직접 비교를 해야하기 때문에 "무식하게 검사하는 방법"으로
위 예시처럼 리스트의 크기가 작으면 괜찮지만
리스트의 크기가 커질수록 비효율적이다.
--
이진 탐색
--
이진 탐색은
(오름차순으로) 정렬된 리스트에서 목푯값을 찾는 알고리즘으로
리스트를 절반으로 분할하고 목푯값이 어느 쪽 절반에 속하는지 결정하는 것을 마지막 값만 남을 때까지 반복한다.
이때 현재 활성화된 탐색 공간(배열)에서 '상계'와 하계'라는 단어도 사용한다.
- 상계 (upper bound) : 현재 활성화된 탐색 공간에 속하는 배열에서 가장 높은 인덱스를 의미
- 하계 (lower bound) : 현재 활성화된 탐색 공간에 속하는 배열에서 가장 낮은 인덱스을 의미
이진 탐색을 매 번 반복할 때마다 현재 활성화된 탐색 공간(배열)의 중간 지점 값을 선택하며 진행한다.
IndexMid = (IndexHigh + IndexLow) / 2
이렇게 중간 지점을 구하고 IndexMid에 위치하는 값과 찾고자하는 목푯값과 비교하여
목푯값이 IndexMid에 위치하는 값보다 작다면 IndexMid를 기준으로 왼쪽 탐색 공간(배열)을 탐색하고
크다면 오른쪽 탐색 공간(배열)을 탐색한다.
만약 같다면 즉시 탐색을 완료한다.

- 현재 활성화된 탐색 공간에서 하계(L)와 상계(H)를 기준으로
중간 지점을 지정(인덱스 = 6)하고 해당 중앙값을 목푯값인 12와 비교.
중앙값보다 목푯값이 크기 때문에 중앙값을 포함하여 좌측 리스트 공간에는 목푯값이 존재하지 않는다고 판단.
우측 리스트만 활성화를 하기 위해 하계를 인덱스 7로 이동. - 변경된 L과 H를 기준으로 중간 지점을 다시 지정(인덱스 = 8)하고 중앙 값을 목푯값인 12와 비교.
중앙값보다 목푯값이 작기 때문에 중앙값을 포함하여 우측 리스트 공간에는 목푯값이 존재하지 않는다고 판다.
좌측 리스트만 활성화를 하기 위해 상계를 인덱스 7로 이동. - 변경된 L과 H를 기준으로 중간 지점을 다시 지정(인덱스 = 7)하고 중앙 값을 목푯값인 12와 비교.
해당 중앙 값이 목푯값과 일치하므로 탐색 완료.
중간 지점을 지정할 때 딱 떨어지지 않는다면 중간 지점에서 좌측에 있는 공간을 중앙값으로 지정한다.
이진 탐색 알고리즘 예시 코드 [JAVA]
public class BinarySearch {
public static int binarySearch(int[] A, int target) {
// 초기 상계와 하계 지정
int indexHigh = A.length - 1;
int indexLow = 0;
while (indexLow <= indexHigh) {
// 중간 지점 계산 (소숫점이 나온다면 해당 소숫점 생략 = 좌측 중간 지점 선택)
int indexMid = (indexHigh + indexLow) / 2;
if (A[indexMid] == target) {
return indexMid;
} else if (A[indexMid] < target) {
indexLow = indexMid + 1;
} else {
indexHigh = indexMid - 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] array = {-5, -2, 0, 2, 5, 9, 12, 15, 16,33, 54, 57};
int target = 12;
int result = binarySearch(array, target);
}
}--
'CS > 자료구조' 카테고리의 다른 글
| 이진 탐색 트리 (0) | 2024.08.05 |
|---|---|
| 스택과 큐 (+ 깊이 우선 탐색, 너비 우선 탐색) (0) | 2024.08.03 |
| 동적 자료 구조 (+ 연결 리스트) (0) | 2024.08.02 |
| 데이터를 메모리에 저장하기 ( + 배열의 삽입 정렬 ) (0) | 2024.07.31 |
| 자료구조란? (0) | 2024.07.30 |
